Spherical projection through GLSL

Spherical projection? In realtime?

When working with a fulldome for realtime 3D projects, one thing is immediately noticeable: this projection surface is not planar. As obvious as it is, it leads to the simple fact that it is not possible for a graphic card to output an image which will not look absurdly deformed once projected. Take a line as a simple example: a straight line becomes a curve when projected on a sphere, so to look straight it has to be deformed before projection and the desired output should be indeed a curve. But a graphic card knows nothing about curves, it can only draw lines, and fill triangles.

Obviously there is a way around this limitation, which is used in every realtime renderers (and in some offline renderers too). The rendering is done in two steps: first a cube map is filled with six renderings for the six directions defined by the cube, then this cube map is applied as a texture on a 3D model representing the mapping of the dome, which is captured and renderer by another camera. This method is derived from cube mapping¹.

This gives us a minimum of seven render pass (you can do with six if your dome is not that ‘full’), which is time and memory consuming. Also it makes the rendering of some visual effects harder, one of them being stereoscopic rendering. This is all the more frustrating as there are work around for offline renderers, which do not have the same graphic card related limitation. Paul Bourke² wrote some interesting articles in this matter.

So, is it possible to create a dome master (that is the name of videos dedicated to fulldome projection) in realtime in a single pass? The answer is kind of a ‘yes, but…’, and this is what makes things interesting.

Shortest path between two points on Earth

Let’s start with the easy part: projecting the vertices onto the spherical camera. This is done through a simple coordinates change, with some scaling to fit the desired dome master coverage. Let’s consider a point \(P = (x, y, z)\) in the standard orthonormal space, its coordinates in spherical space would be:

These coordinates can then be converted easily into screen space, first by getting sending \(r_P\) into the depth buffer (with or without a prior transformation to manage where we need precision), then by transforming the other two coordinates to fit \([-1; 1]\):

All is well, we can now draw our vertices / polygons in a spherical space. Let’s try to implement it as a vertex shader and see what it gives. In the following example we only want to keep half of a sphere which is why we divide by \(\pi\), but it could be any value (higher than 0.0 and lower or equal to \(2\pi\):

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#define PI 3.14159265358979323846264338327

/***************/
float sinCosRestrain(in float v)
{
    return max(-1.0, min(1.0, v));
}

/*************/
vec4 toSphere(in vec4 v)
{
    float val;
    vec4 o = vec4(1.0);

    float r = sqrt(pow(v.x, 2.0) + pow(v.y, 2.0) + pow(v.z, 2.0));
    val = max(-1.0, min(1.0, v.z / r));
    float theta = acos(val);

    float phi;
    val = v.x / (r * sin(theta));
    float first = acos(sinCosRestrain(val));
    val = v.y / (r * sin(theta));
    float second = asin(sinCosRestrain(val));
    if (second >= 0.0)
        phi = first;
    else
        phi = 2.0 * PI - first;

    o.x = theta * cos(phi);
    o.y = theta * sin(phi);
    o.y /= PI;
    o.x /= PI;

    return o;
}

Here is an example result of a plane rendered with such a shader:

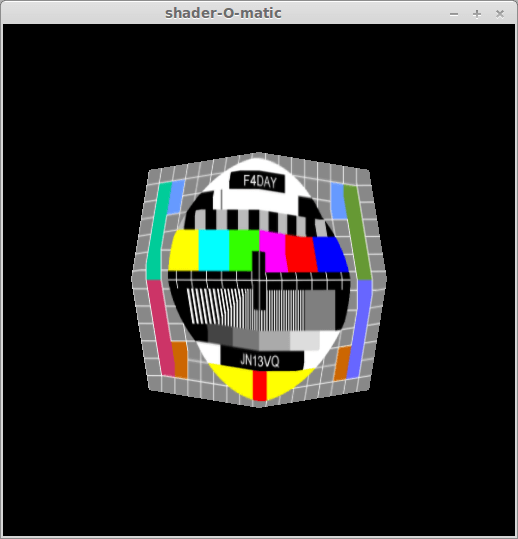
Hum. This looks very edgy for a spherical projection. This simple plane does not look like a plane any more, even in our new space. When projected on a sphere, a line becomes a curve and this is definitely not what we see here. This is due to how a graphic card draws edges and triangles: it knows nothing but straight lines. And it certainly does not know that we are working in a spherical space.

Before going further, one should be aware that this is kind of a bruteforce method, as we completely override optimizations of graphic cards, but it is too soon for optimization.

Subdivide!

So we have to handle the fact that a graphic card can only draw lines. Indeed, the curve we wish we got through the spherical projection is more complex than a straight line, and this complexity is lost through the projection of its two end vertices. One solution though is to simulate this complexity by adding geometry where there is none, which means by adding vertices between the end vertices.

Our initial solution was implemented through a vertex shader. Since OpenGL 3.0 (and even a bit earlier through specific extensions), GLSL offers us the possibility to add geometry on the fly, using a geometry shader. The method I used is rather simple:

• Subdivide an edge in two parts,
• if not subvdivided enough, repeat,
• project the resulting bunch of vertices in spherical space,
• grab another edge to process.

A few things to know though. Firstly, it is not possible to do recursive function call in GLSL, so you have to declare as many identical functions as the maximum subdivision level you want. Secondly, geometry shaders were never meant to add lots of geometry, so performance drops drastically when the subdivision level gets high. Moreover the maximum number of vertices a geometry shader can output is fairly low (depending on the hardware / driver, but don’t count on anything higher than 128). Anyway, subdividing three times gives already good results:

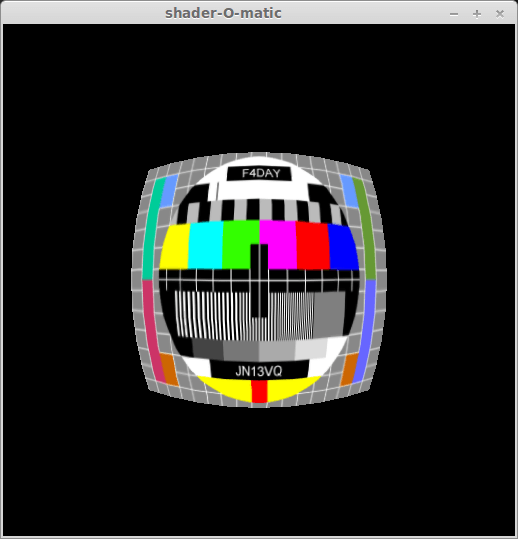
Discussion

This is a quite obvious way to create a dome master, the smart move being in the subdivision. But it is clearly a prototype and not meant to be used in production as-is. A few things I can think of that should be dealt with before that:

• Performance. I did no extensive testing, but this shader shows lots of roots and trigonometric functions.
• Quality. More and more targeted subdivisions by replacing the geometry shader by a tessalation shader.
• Reproduction of common effects. Or at least basic shading, in spherical coordinates.

But this approach is still interesting in that it reduces gpu memory bandwidth consumption, and opens the path to stereoscopic spherical projections.